Explore Simple Game Algorithms with Color Walk: Part 4

In this series we are taking a look at different game algorithms using the simple game Color Walk as a sandbox for exploration and discovery. The last post showed how to add multiple algorithms and select between them, as well as exploring a random choice algorithm and an enhanced way to skip useless choices for both round-robin and random choice. This post will get into our first non-trivial algorithm, the greedy algorithm. Greedy algorithms don't care too much about the future. They will look at the choices immediately in front of them and try to pick the choice that will get them the most stuff right away. That's why they're called greedy, you see? In this case, the greedy algorithm will pick the color that will remove the most blocks on the next turn. Let's see how it stacks up to the trivial algorithms.

Getting Greedy

The greedy algorithm will require some changes to the color controls so that we can query for how many blocks each color will remove. The algorithm will ask each control how many blocks will be removed with Control.checkGameBoard(), but currently that function only returns true or false depending on if there are any matching blocks or not. Here's what it looks like right now:

    this.checkGameBoard = function(only_check) {
      var match = false;
      var color = this.color;

      _.each(blocks, function (block) {
        if (block.isDead) {
          match = match || getNeighbors(block, color, only_check);
        }
      });

      return match;
    }

One option for modifying it to keep track of how many blocks would be removed would be to tally the matches within the calls to getNeighbors() and checkNeighbors(), but getting the tally right without double-counting is complicated. An easier method is to mark the blocks that match while searching through all of the blocks, and count them after they've all been checked. To do this marking, we need to add a property to Block because we don't want to use isDead to keep track of potentially removed blocks, only actually removed blocks. It would get complicated trying to back out those blocks that were marked only when checking and not actually making a move. After adding a Block.marked property:

  function Block(x, y, color, i, isDead) {
    this.x = x;
    this.y = y;
    this.color = color;
    this.position = i;
    this.isDead = isDead;
    this.marked = isDead;

We can modify Control.checkGameBoard() to initialize each block.marked property, run the check, and then count the newly marked blocks:

    this.checkGameBoard = function(only_check) {
      var color = this.color;
      _.each(blocks, function (block) {
        block.marked = block.isDead;
      });

      _.each(blocks, function (block) {
        if (block.isDead) {
          getNeighbors(block, color, only_check);
        }
      });

      var new_marked_count = _.filter(blocks, function (block) {
        return (block.isDead != block.marked);
      }).length;

      return new_marked_count;
    }

Counting the newly marked blocks is easy. They are simply the blocks that are marked, but not dead. The _.filter() function does the job nicely. Notice that the match variable was removed because we don't want to end the check early anymore, and if Control.checkGameBoard() returns a nonzero value, then we know there was at least one match for the other algorithms that still need that information. We should be sure to change those algorithms accordingly:

    this.roundRobinWithSkipping = function() {
      do {
        this.index = (this.index + 1) % controls.length;
      } while (controls[this.index].checkGameBoard(true) === 0);
    }

    this.randomChoiceWithSkipping = function() {
      do {
        this.index = randomInt(0, controls.length - 1);
      } while (controls[this.index].checkGameBoard(true) === 0);
    }

Continuing with the changes to Control.checkGameBoard(), we need to fix up the functions called inside this function. Control.getNeighbors() only change is that it no longer needs to return a value:

    function getNeighbors(block, color, only_check) {
      // ...

      checkNeighbors(neighbor_positions, color, only_check);
    }

Control.checkNeighbors() requires a few more changes. Here is what it looked like before:

    function checkNeighbors(positions, color, only_check) {
      var match = false;
      _.each(positions, function (position) {
        var block = blocks[position];
        if (block.color == color && !block.isDead) {
          if (only_check) {
            match = true;
            return;
          }
          block.isDead = true;
          $('#block' + position).css('background-color', '#d9d9d9');
          getNeighbors(block, color, only_check);
        }
      });

      return match;
    }

Now we no longer need the match variable, and we don't want to return immediately when a match is found. Instead, if we're only checking, we'll mark the block. Otherwise, we'll set the block to be dead and change its color. In both cases, we'll call Control.getNeighbors() again to continue the search:

    function checkNeighbors(positions, color, only_check) {
      _.each(positions, function (position) {
        var block = blocks[position];
        if (block.color == color && !block.isDead && !block.marked) {
          if (only_check) {
            block.marked = true;
          } else {
            block.isDead = true;
            $('#block' + position).css('background-color', '#d9d9d9');
          }
          getNeighbors(block, color, only_check);
        }
      });
    }

At this point Control.checkGameBoard() is returning the number of matched blocks, so we're ready to add the logic for the greedy algorithm. We have to add it to the list:

      $('#solver_type').change(function () {
        switch (this.value) {
          // ...
          case 'greedy':
            that.solverType = that.greedy;
            break;
          default:
            that.solverType = that.roundRobin;
            break;
        }

Then we can add the function to implement it:

    this.greedy = function() {
      max_matches = 0;
      max_index = 0;
      _.each(controls, function(control, i) {
        matches = control.checkGameBoard(true);
        if (matches > max_matches) {
          max_matches = matches;
          max_index = i;
        }
      });
      this.index = max_index;
    }

The greedy algorithm does just what we said it would. It looks at each control for how many blocks will be removed. If it's more blocks than already found, the max_matches and max_index are updated. After all controls are searched, the control index is set to the one that removes the most blocks. This implementation is okay, but it could be more elegant. Underscore has a _.max() function that would be just what we need, but it only returns the control associated with the maximum value returned from the function passed to it. That means we lose track of which index corresponds to the control that removes the most blocks. To fix this problem, we can add the index as a property to each control, so that we can get it back from the control later. The reworked algorithm looks much cleaner:

    this.greedy = function() {
      max_control = _.max(controls, function(control) {
        return control.checkGameBoard(true);
      });
      this.index = max_control.index;
    }

Just make sure to add the index property and initialize it when creating the controls:

  _.each(colors, function (color, i) {
    controls.push(new Control(color, i));
  });

  // ...
  function Control(color, index) {
    this.color = color;
    this.index = index;

Okay, everything is ready now. How does the greedy algorithm perform?

It does pretty well! When the algorithm is running, it looks similar to the round-robin with skipping, with the blocks being swept off the board, generally from left to right. Sometimes certain colored blocks will remain as stragglers for a split second, but overall, it gives the impression of running quite fast and smooth. The following table shows how the greedy algorithm stacks up to the other algorithms:

Algorithm	Min	Mean	Max	Stdev
Round Robin	37	48.3	62	4.5
RR with Skipping	37	46.9	59	4.1
Random Choice	60	80.2	115	10.5
Random with Skipping	43	53.1	64	4.5
Greedy	31	39.8	48	3.5

Clearly, the greedy algorithm significantly improves upon all the other algorithms in every way. It's minimum number of moves is six moves better than the second best algorithm, it's maximum number of moves is eleven moves better, and it's standard deviation is substantially tighter. All of these improvements were achieved by simply picking the color on each move that resulted in the most progress without looking more than one move ahead. Greedy algorithms normally perform quite well, considering their simplicity, and they tend to be fast because they don't spend any time evaluating options farther in the future.

The choice of what to optimize for the greedy algorithm can make a difference, and here the choice was relatively easy. Since we're trying to clear the board of colored blocks, the number of blocks cleared on a move is an obvious parameter to optimize. But there are others, and we'll explore some other choices in later posts. Right now it will be interesting to look at what happens when we extend the greedy algorithm to look ahead to more moves.

Getting More Greedy

Logically, if we can make the greedy algorithm take into account what happens to the board in future moves, we should be able to improve its performance further. If choosing a certain color on the current move doesn't remove the most blocks, but opens up more blocks to be removed on the next turn, that could be a better choice than picking the color that removes the most blocks right away. We'll call such a strategy greedy-look-ahead, and the looking ahead doesn't need to be limited to one extra move. Conceptually, the algorithm could look ahead as many moves as possible to attempt to find the optimal sequence of moves.

In generalizing the greedy-look-ahead algorithm, we can think of searching the set of move sequences like searching a tree where each node in the tree is a board position with some number of blocks cleared, and each branch from a node is a different move with its associated color choice. The ultimate goal is to find the shortest path from the current node to a leaf node, which is an empty board. Thinking of greedy-look-ahead as a tree or graph search algorithm opens up a number of other algorithms for consideration, but that's getting a little ahead of ourselves at this point. It's important to see the connection between the logical extension of the greedy algorithm and the field of graph algorithms, but for now we'll leave it at that. We still need to figure out how to extend the greedy algorithm by looking ahead even one move.

Looking ahead with the greedy algorithm (or any algorithm, for that matter) presents an immediate problem. How do we explore a move after one move choice, and then back up to explore another move that's still after that same first move? We want to only partially restore the board state when iterating through second moves, otherwise we're doing the same work of finding marked blocks for the first move multiple times. We already solved this issue for analyzing the first move in the greedy algorithm by adding the Block.marked property, but we don't want to have to add another property for every move that we want to look further ahead. Maybe we can modify the Block.marked property to contain the move number that it was marked on. That way we can easily remove the marks on blocks corresponding to certain moves. Implementing this behavior in Control.checkGameBoard() would look something like this:

    this.checkGameBoard = function(check_move) {
      var color = this.color;
      _.each(blocks, function (block) {
        if (block.marked >= check_move) {
          block.marked = 0;
        }
      });

      _.each(blocks, function (block) {
        if (block.isDead || (block.marked < check_move && block.marked !== 0)) {
          getNeighbors(block, color, check_move);
        }
      });

      var new_marked_count = _.filter(blocks, function (block) {
        return (0 !== block.marked);
      }).length;

      return new_marked_count;
    }

Something has changed in each section of code, so let's carefully go through it. First, the only_check function parameter has changed to check_move to better describe its new role. Instead of specifying that the board will be either checked only or also have blocks cleared, it now specifies for which move the check is occurring. If check_move === 0, then we are doing the actual move that clears blocks instead of just checking.

In the first _.each() code block, instead of initializing every block.marked value to its corresponding block.isDead value, we are searching for block.marked values that are greater than or equal to the move number that is currently being checked. We know that since we are checking a certain move number, any marked move numbers equal to or above that should be cleared before we check the game board on this go around, since we've backed up to a previous move or we're checking the same move with a different color control.

In the second _.each() code block, we need to expand the set of blocks that we're looking at the neighbors of to see if they should be marked. Before when we were checking the board, we could be sure that dead blocks were the same as marked blocks, but now we could have blocks that aren't dead but are marked for subsequent potential moves. These blocks should be considered dead for the purposes of this check, but only if they are marked with a move less than the current move. There's no need to re-check the neighbors around blocks that have been marked as cleared during the current run of the board check. This whole line of reasoning leads to the extra condition of (block.marked < check_move && block.marked !== 0).

Finally, in the count of how many blocks have been marked, instead of comparing against block.isDead, we want to count how many blocks have been marked on any move. This way any check of the board will return the number of blocks cleared for the full sequence of moves that has been explored so far, and we won't need to keep track of a block tally higher up in the algorithm.

With Control.checkGameBoard() changed, we can move along to getNeighbors(). The changes here are minor, with renaming only_check to check_move being the only change. The next changes occur in checkNeighbors():

    function checkNeighbors(positions, color, check_move) {
      _.each(positions, function (position) {
        var block = blocks[position];
        if (block.color === color && !block.isDead && block.marked === 0) {
          if (check_move > 0) {
            block.marked = check_move;
          } else {
            block.isDead = true;
            $('#block' + position).css('background-color', '#d9d9d9');
          }
          getNeighbors(block, color, check_move);
        }
      });
    }

The function parameter only_check is again renamed to check_move, and then we have to be careful which blocks we mark as being cleared on this move. Now, instead of unmarked blocks being set to false, they are set to zero, so the end of the conditional for finding a matching block changed to correspond to that behavior. Then, we want to mark matching blocks if check_move is not zero. In that case we mark the block with the move we are checking for. Otherwise, we clear the block for real, as we were doing before.

Other than those changes, we need to initialize Block.marked to zero and fix the calls to Control.checkGameBoard(). Any false arguments should be changed to 0, and true arguments should be changed to 1.

At this point all of the algorithms should work as they did before, and we are ready to add the greedy-look-ahead algorithm. This set of code changes is yet another example of making the change easy, and then making the easy change. To add the new algorithm, we make another entry in the HTML select control and add it to the switch statement:

      $('#solver_type').change(function () {
        switch (this.value) {
          // ...
          case 'greedy-look-ahead':
            that.solverType = that.greedyLookAhead;
            break;
          default:
            that.solverType = that.roundRobin;
            break;
        }

Then we can add the algorithm logic, where the logic is very similar to the greedy algorithm, but we want to look one move deeper than before:

  function Solver() {
    // ...

    this.greedyLookAhead = function() {
      var max_control = _.max(controls, function(control1) {
        control1.checkGameBoard(1);
        var matches = _.map(controls, function(control2) {
          return control2.checkGameBoard(2);
        })
        return _.max(matches);
      });
      this.index = max_control.index;
    }

Instead of having the _.max() iterator function return the number of matches for each color control, we check the move for the color control passed to the function, and then make an array with _.map() of the matches that result from using each color control for the second move. Then we return the maximum value of this array of matches as the value that should be maximized to pick the control for the real next move. It's a nice, straightforward extension of the greedy algorithm. The problem is, it won't work. Can you spot the problem?

What happens at the end of the game when there is only one color block left on the board? If the blocks are the turquoise color of the first control, everything will be fine because that color will be chosen for the control to use on the next move anyway. But, if it's any other color, the first color control will still be chosen because the board will get cleared on the second move for sure, because every control is cycled through on the second move, and the color of the last remaining blocks will be one of them. Since the first control will always be chosen for the next move, the algorithm gets into an infinite loop.

The easiest way to fix this problem is to have the algorithm skip controls that result in zero blocks removed, like in the modified round-robin and random choice algorithms. If those controls are skipped, then moves will never be chosen that don't result in at least one block being removed, so the algorithm will always make forward progress. When there's only one color block left on the board, forward progress means clearing the board. We also improve the speed of the algorithm somewhat by not looking at useless moves. Here's what the modified algorithm looks like:

    this.greedyLookAhead = function() {
      var max_control = _.max(controls, function(control1) {
        if (control1.checkGameBoard(1) === 0) {
          return 0;
        }
        var matches = _.map(controls, function(control2) {
          return control2.checkGameBoard(2);
        })
        return _.max(matches);
      });
      this.index = max_control.index;
    }

With the algorithm now working, we can test it out:

Then we can see how it stacks up against the rest of the algorithms:

Algorithm	Min	Mean	Max	Stdev
Round Robin	37	48.3	62	4.5
RR with Skipping	37	46.9	59	4.1
Random Choice	60	80.2	115	10.5
Random with Skipping	43	53.1	64	4.5
Greedy	31	39.8	48	3.5
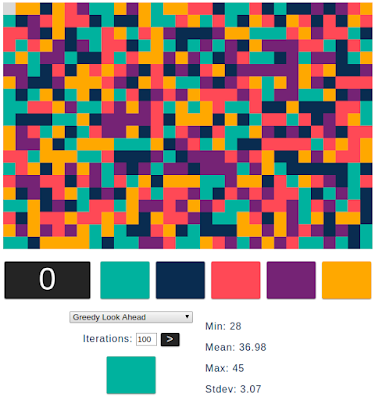
Greedy Look Ahead	28	37.0	45	3.1

Looking ahead one extra move improved the min, mean, and max by three moves, and tightened the standard deviation by 0.4 moves. We also broke 30 moves for the first time, something that's reasonably difficult to do when playing Color Walk manually. Notice that looking one move ahead had diminishing returns, though. Whereas the greedy algorithm improved over round-robin with skipping by six to eleven moves, adding look ahead made less than half that improvement. It's likely that looking farther ahead will give less and less improvements, and the algorithm will have to work harder and harder to achieve those improvements because of the exponential growth of moves to look at.

It was already obvious from watching the algorithm run in batch mode that looking one move ahead was starting to slow it down compared to the base greedy algorithm. Every extra move we look farther ahead increases the number of moves we need to look at by a factor of four because the move tree branches out by four color controls on each move. This exponential growth likely means that we can reasonably look ahead only about four or five moves with the current data structure that we're using, but we may be able to improve on that by using a data structure that shortens the time we spend searching for color matches. That will be an exercise for next time.

So we've seen our first non-trivial algorithm with the greedy algorithm, and it turns out that it performs quite well. With an extra one-move look ahead, it improves on the previous best algorithm, round-robin with skipping, by over 20%, on average. We're now ready to push the greedy algorithm even further by cranking up the number of moves that it looks ahead and optimizing the search speed for finding color matches. Next time we'll look at a better data structure for the board and see how far we can push the greedy algorithm.


Article Index
Part 1: Introduction & Setup
Part 2: Tooling & Round-Robin
Part 3: Random & Skipping
Part 4: The Greedy Algorithm
Part 5: Greedy Look Ahead
Part 6: Heuristics & Hybrids
Part 7: Breadth-First Search
Part 8: Depth-First Search
Part 9: Dijkstra's Algorithm
Part 10: Dijkstra's Hybrids
Part 11: Priority Queues
Part 12: Summary

Share this post